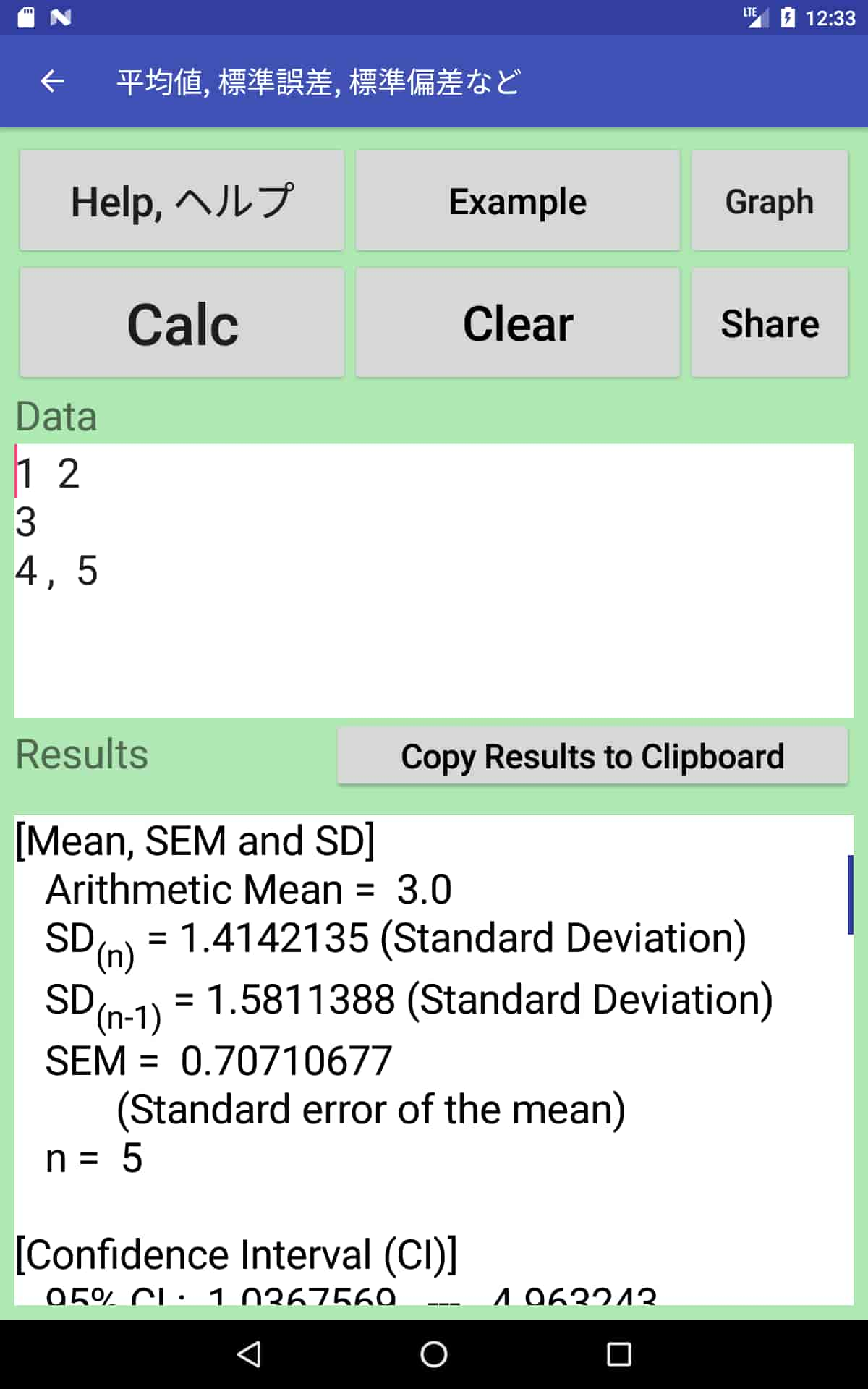
Stats testerとRの検定結果の比較

 

1. 例題はStats testerアプリのExampleボタンタップで入力されるデータです。
2. Stats testerのCalcボタンをタップすると、出力窓の最後にp値が表示されます。
3. MacやWindows PCなどでR言語をお使いの場合は、Code の数行をまとめてコピー／ペーストして実行すると、Rの出力結果のp-valueにp値が表示されます。

 

3. 「1標本 t-検定（基準値との比較）」

例題
  A : 1, 3, 2, 5, 6, 11
  比較する平均値 : 8
Stats tester
  p = 0.073464 (2 tails)
R
  Code:
    A <- c(1,3,2,5,6,11)
    mu <- 8
    t.test(A, mu=8, alt="two.sided")
  Result
    p = 0.0734649 (2 tails)

 

4. 「二標本t-検定（独立２群） 」

例題
  A : 1, 2, 3, 4, 5
  B : 11, 13, 15, 17
Stats tester
  Student p = 0.000097 (2 tails)
  Welch p = 0.000846 (2 tails)
R
  Code:
    A <- c(1, 2, 3, 4, 5)
    B <- c(11, 13, 15, 17)
    t.test(A, B, alt="two.sided",var.equal=T) # (Student)
    t.test(A, B, alt="two.sided",var.equal=F) # (Welch)
  Result
    Student p = 0.000097 (2 tails)
    Welch p = 0.0008459 (2 tails)

 

5.「対応標本のt-検定（対応2群）」

例題
  A : 22, 20, 31, 25
  B : 11, 15, 28, 20
Stats tester
  p = 0.040519 (2 tails)
R
  Code:
    A <- c(22, 20, 31, 25)
    B <- c(11, 15, 28, 20)
    t.test(A, B, paired=T, alt="two.sided")
  Result
    p = 0.04052 (2 tails)

 

6. 「1元配置分散分析 （1-way ANOVA）」

例題
  A : 13, 12, 11, 11
  B : 9, 8, 9, 7, 10
  C : 12, 14, 11, 13
  D : 13, 14, 13, 15
Stats tester
  p = 0.000059
R
  Code:
    vx <-c(13, 12, 11, 11, 9, 8, 9, 7, 10, 12, 14, 11, 13, 13, 14, 13, 15 )
    fx=factor(rep(c("A", "B", "C", "D"), c(4, 5, 4, 4)))
    anova(aov(vx~fx))A
  Result
    p = 5.874e-05

 

7. 「ピアソンの相関係数の検定、直線回帰」

例題
  A : 1, 4, 4, 6, 8
  B : 5, 8, 7, 10, 11
Stats tester
  p = 0.003436 (2 tails)
R
  Code:
    A <- c(1, 4, 4, 6, 8)
    B <- c(5, 8, 7, 10,11)
    cor.test(A, B, method="pearson")
  Result
    p = 0.003436 (2 tails)

 

8. 「シャピロ・ウィルク検定とQ-Qプロット」

例題
  A : 1, 2, 3, 3.9, 4.2, 4.5, 5, 5.4, 5.6 ,5.8, 6.2, 6.4, 6.6, 7, 7.5, 7.8, 8.1, 9, 10, 11
Stats tester
  p = 0.999942
R
  Code:
    A <- c(1, 2, 3, 3.9, 4.2, 4.5, 5, 5.4, 5.6 ,5.8, 6.2, 6.4, 6.6, 7, 7.5, 7.8, 8.1, 9, 10, 11)
    shapiro.test(A)
  Result
    p = 0.999942

 

9. 「カイ2乗検定（2x2 独立性）」

例題
  110, 90
  88, 112
Stats tester
  p = 0.035720 (Continuity corrected)
  p = 0.027799 (Continuity not corrected)
R
  Code:
    table <- matrix(c(110, 90, 88, 112), ncol=2, byrow=T)
    chisq.test(table, correct=T)
    chisq.test(table, correct=F)
  Result
    p = 0.03572 (Continuity corrected)
    p = 0.027799 (Continuity not corrected)